Article Text
Abstract
In-hospital fall incidence is a critical indicator of healthcare outcome. Predictive models for fall incidents could facilitate optimal resource planning and allocation for healthcare providers. In this paper, we proposed a tensor factorisation-based framework to capture the latent features for fall incidents prediction over time. Experiments with real-world data from local hospitals in Hong Kong demonstrated that the proposed method could predict the fall incidents reasonably well (with an area under the curve score around 0.9). As compared with the baseline time series models, the proposed tensor based models were able to successfully identify high-risk locations without records of fall incidents during the past few months.
- digital health
- data mining
- fall prevention
- inventions
- machine learning
This is an Open Access article distributed in accordance with the Creative Commons Attribution Non Commercial (CC BY-NC 4.0) license, which permits others to distribute, remix, adapt, build upon this work non-commercially, and license their derivative works on different terms, provided the original work is properly cited and the use is non-commercial. See: http://creativecommons.org/licenses/by-nc/4.0/
Statistics from Altmetric.com
Introduction
The incidence of falls is a commonly used indicator of healthcare outcome. Injuries related to falls are the most common causes of accidental death for individuals over the age of 65 years in the USA and many developed countries.1 Fall prevention is a major challenge in the care continuum, especially for in-hospital patients. The incidence of in-hospital fall has drawn recent attention due to the ageing population and limited resources for public health systems.2
Researchers have categorised risk factors for inpatient falls into patient-related factors (such as age and cognitive function) and treatment-related factors (such as admission department functions).3 Existing research on fall prevention mainly relies on the analysis of patient-related factors obtained with criterion-referenced assessment tools, like balance and mobility tests.4 For instance, Neumann et al 5 evaluated the performance of two fall risk screening methods to identify high-risk groups using a retrospective analysis of hospitalised patients. Kim et al 6 evaluated three fall assessment tools to identify patients at high risk for falls. Schwendimann et al 7 researched on the fall incidents across multiple clinical departments in hospitals and found that the occurrence of inpatient falls was largely varied among different departments. In particular, department-specific system on patients at risk of fall has been implemented in departments including Orthopaedics & Traumatology, Clinical Oncology and Medicine in Hong Kong.8 Studies showed that themes such as information systems for falls and guidance of the prevention programme by a multidisciplinary committee were associated with successful implementation of fall prevention programmes.9
There are a number of data mining studies focusing on predicting the fall incidence of different cohorts. Hill et al 10 conducted a field study to identify the common features in falls incidents and explored the feasibility of predicting falls using a multivariate logistic regression model. Hausdorff et al 11 explored the potential use of gait variability to evaluate the prospective fall risk in community-living older adults. In another study, Stalenhoef et al 12 identified a set of important intrinsic risk factors for fall incidents. Halfon et al investigated the Poisson regression model for fall incidents (first fall during a hospitalisation). Their study presented that Poisson modelling is appropriate without overdispersion.13 Marschollek et al 14 exploited the data mining methods for fall prediction of geriatric inpatients’ assessment data. The two adopted classification models (decision tree and logistic regression model) were able to identify around half of the patients who would suffer a fall during their stay in hospital, making them not applicable to fall preventions.
Because of the small sample size of longitudinal data and the complexity of the data of hospital operations and individuals’ health conditions, it is very difficult to identify representative data and proper methods for reliable fall prediction. In fact, existing studies may not be able to achieve better performance than a simple clinical judgement of risk of falls.15 This research aims at location-specific fall prediction instead of prediction for individual patient. In addition, typical time series models make prediction with historical data. The disadvantage is that such models could not predict the incidents at specific location without fall records. This research aims to fill this important knowledge gap through using structured data of fall incidents reports from public hospitals to predict the occurrence of falls at different locations and departments in hospitals. To accomplish this task, we focused on using treatment-related factors to inpatient fall predictions instead of patient-related factors.
The department and hospital of patients are related to the falls at different locations because of the characteristics of patients and healthcare services. For example, patients in Medicine and Geriatrics department are mostly older adults with balance and mobility impairment who are at high risk of falls. For another example, certain hospitals could have recently installed newer fall prevention facilities (like warning signs, chrome knurled grab bars and so on). The fall incidents are usually associated with the workload of the hospital staff. Therefore, the implementation of fall prevention programmes could also change the risk of different locations. For example, hospitals may make changes of the nursing practice to increase the nurse patient ratio; the patient would be assisted to the toilet by staff with commode chair. This practice could reduce the risk of fall at bedside, making toilet with higher risk on the other hand. Therefore, predicting the occurrence of falls in different locations could help health providers to develop proactive prevention strategies to effectively allocate resources and implement prevention programmes for high-risk locations. The proposed method could potentially benefit healthcare operations, answering practical questions like ‘Is there a risk of falls at the bedside in the Medicine & Therapeutics department in Hospital A in next month?’ or ‘Which location in the department are facing an increasing risk of falls?’.
Different from previous research, our study explored a novel tensor factorisation-based approach to predicting fall incidents across different departments and locations. In particular, the advantage of tensor factorisation-based models is the capability to capture the inherent relations between patients, locations and other information without explicitly incorporating patient characteristics.16 Tensor factorisation is the higher order extension of matrix factorisation that provides a powerful framework for various applications including biomedical data mining and precision medicine.17 18
In this research, we proposed a fourth-order tensor factorisation-based method to capture the latent relations between the four dimensions of attributes in the fall incidents data for reliable fall prediction over time. The record of fall incidents maintained by hospitals contains important information of the identity and characteristics of patients, the time of the incidents, the locations and departments of falls. This location-based information of in-hospital fall incidents has not been fully used for fall prediction. In particular, we evaluated the model using the fall in seven public hospitals in Hong Kong, from January 2014 to September 2014. The data contains the following information: (A) time and date of the fall incidents, (B) the location of falls (eg, bedside and toilet), (C) department (eg, surgery and medicine) and (D) hospital.
Data and methodologies
Data
In this research, we used the fall incidents data from seven public hospitals in Hong Kong from 1 January 2014 to 30 September 2014. The data contains occurrence date and time, department and specific location (eg, bedside and toilet) of each fall incident. The identity-related information of patients was excluded from the dataset. Figure 1 presents a hypothetical example of one incident in the dataset. In the table, ‘Case_No’ is the identifier of the incident. ‘Occ_Dt’ and ‘Occ_Time’ represent the date and time when the incident occurred. ‘Location’ represents the specific location in the hospital where the incident occurred. ‘Rep_Dept’ represents the hospital department of the patient.
- Download figure
- Open in new tab
- Download powerpoint
One incident in the dataset (hypothetical data).
Methodologies
Tensor factorisation
Tensors are multidimensional arrays describing the linear relations between objects. Tensors provide a natural mathematical framework for representing and solving problems in a wide range of areas. Tensor factorisation is the higher order extension of matrix factorisation, which is able to capture the latent patterns in multiway datasets.19 Tensor factorisation (or tensor decomposition) has been successfully applied to a rich set of data mining problems including computer vision, link prediction, recommender systems, precision medicine and and so on.17 20–22 The most widely used decomposition methods are CANDECOMP/PARAFAC (CP) decomposition and Tucker decomposition.19 The Tucker decomposition, also referred as higher order singular value decomposition (SVD), or M-model SVD, decomposes a tensor into a core tensor multiplied by a matrix along each mode. CP decomposition decomposes the tensor into the sum of rank one tensors. CP decomposition is a special case of Tucker decomposition, whose core is superdiagonal.
CP decomposition is a highly interpretable factorisation that can be used to address the temporal prediction problems. In addition, CP is unique under very mild assumptions,23 making it suitable to uncover and interpret the actual latent factors. Different from CP, matrix SVD is not unique unless all singular values are distinct. Therefore, compared with matrix decompositions and Tucker, CP has an advantage because, in general, there is no equivalent rotated decomposition yielding the same fit.24 For the rest of this paper, we adopted CP decomposition to factorise the tensor.
To illustrate tensor factorisation, we present the decompositions of matrix, third-order tensor and fourth-order tensor in figure 2. Typically, a matrix could be decomposed to the sum of a number of rank-1 components as shown in figure 2A. Similarly, CP decomposition method decomposes a tensor into the summation of a number of rank-1 tensors, as illustrated by figure 2B,C. In this research, we perform CP decompositions of fourth-order tensors, so we use 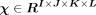 to represent a fourth-order tensor for illustration purpose.
to represent a fourth-order tensor for illustration purpose.
- Download figure
- Open in new tab
- Download powerpoint
An illustration of the decomposition of (A) matrix, (B) the third-order tensor and (C) the fourth order tensor.
Therefore, a fourth-order tensor can be expressed as follows,
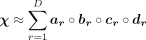 (1)
(1)
where  denotes the outer product,
denotes the outer product, 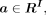
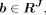
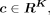
 are feature vectors in four dimensions. The entry in the tensor can also be written as
are feature vectors in four dimensions. The entry in the tensor can also be written as
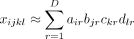 (2)
(2)
With a proper estimation of these latent feature vectors a, b , c and d based on known entries, we could use the factorised features as a predictor of unobserved entries in X.
Simple moving average (SMA)
SMA is a useful forecasting method for predicting the time series, particularly when there is no observed seasonality.25 Given time series Yt
, the value of 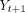 is estimated as the average of data in the previous N time periods. The calculation is expressed as
is estimated as the average of data in the previous N time periods. The calculation is expressed as
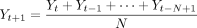 (3)
(3)
Exponentially weighted moving average (EWMA)
EWMA is a method using a weighted average of the past observations.26 Different from SMA, the weight for older historical data decreases exponentially and could react to the change trend of data, particularly recent patterns with a higher sensitivity. In this research, we adopted EWMA to calculate the prediction as follows:
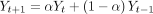 (4)
(4)
where  is the smoothing coefficient.
is the smoothing coefficient.
Proposed tensor-based method
In this study, we developed models to incorporate the CP factorisation results with SMA and EWMA methods to predict the future fall incidence. Because we focused on location-specific fall prediction, plus we do not have information of patients’ identity, we did not include personal information of patients in our models. Instead, we aimed to model the temporal patterns of fall incidence at specific locations. As discussed in the introduction section, the department and hospital that patients belong to are related to the falls at different locations because such information could imply the different characteristics of patients and healthcare services. Therefore, the location-specific data used in this method includes location, department and hospital. The multiway relations between locations, departments and hospitals could be naturally represented as a third-order tensor as shown in figure 3.
Tensor representation of fall incidents data.
Then, the temporal patterns could be represented using a fourth dimension. In this case, we can define a tensor X of size 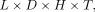 such that
such that
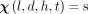 (5)
(5)
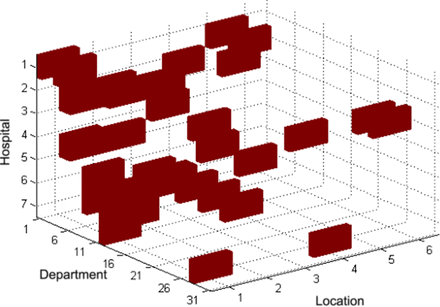
where 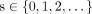 represents the number of fall incidents occurred at location l of department d in hospital h at time t. The goal of this research is to estimate the risk of fall incidence and predict the occurrence of fall at a single time period T+1 by analysing the tensor for each period of time T,…,T−N+1. Figure 4 illustrates such a fourth-order tensor data for our dataset from January 2014 to September 2014.
represents the number of fall incidents occurred at location l of department d in hospital h at time t. The goal of this research is to estimate the risk of fall incidence and predict the occurrence of fall at a single time period T+1 by analysing the tensor for each period of time T,…,T−N+1. Figure 4 illustrates such a fourth-order tensor data for our dataset from January 2014 to September 2014.
- Download figure
- Open in new tab
- Download powerpoint
Illustration of the fourth-order tensor.
As introduced in earlier in this section, the fourth-order tensor could be factorised as the summation of D rank-1 components, and each component is the outer product of four latent feature vectors.
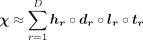 (6)
(6)
And each entry in the original tensor is approximated as below
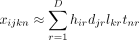 (7)
(7)
CP decomposition has the advantage of interpretability to extract the latent factors to capture the clustering information of certain hospitals, departments, locations and, particularly, the temporal information in the latent feature vector tr . The extension to the fourth-order tensor enables further processing of the temporal dimension for prediction over time as shown in figure 5.
- Download figure
- Open in new tab
- Download powerpoint
Illustration of temporal prediction based on fourth-order tensors.
The values in the tensor are the number of fall incidents at each location during a time period. So, we used the commonly used Poisson distribution to model the count data.13 Therefore, two non-negative CP decomposition methods under the Poisson distribution assumption were adopted in our methods. One is the Non-negative Multiple Tensor Factorization (NMTF) that employed the generalised Kullback-Leibler divergence and multiplicative update rules.27 The other is the CP Alternating Poisson Regression (CP-APR) based on a majorisation–minimisation approach for multilinear modelling of sparse count data.28
After we factorised the tensor, we applied an SMA-based heuristic approach proposed in Dunlavy et al’s study20 to generate a risk score for predictions. SMA method is simple but usually very effective when there is no clear seasonality and trend. Similar to the equation 15 in Dunlavy et al,20 we calculated the fall risk score for each location as follows:
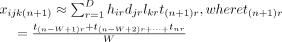 (8)
(8)
In addition, we also proposed another model using EWMA instead of SMA. The prediction of the temporal dimension could be calculated recursively in the selected sliding window.
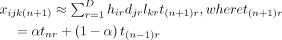 (9)
(9)
The risk score is set to be the predicted number of fall incidents for corresponding location. We can rank the score of each location to identify those with high risk of fall incidents.
Results
In order to validate the effectiveness of the proposed tensor-based method, we performed two experiments with the 9-month in-hospital fall incident data. In the first experiment, we used a 3-month sliding window (N=3) for forecast: we used the proposed method to predict the fall incidents in a month using the data of last 3 months. In the second experiment, we used a 5-month sliding window (N=5) to predict the fall incidents in a month using the data of last 5 months. The reason we chose these two sliding windows is as follows: (A) if the sliding window was too narrow (eg, N=1 or N=2), we could not get sufficient data to forecast. If the sliding window is too broad (eg, N=7 or N=8), we could not get sufficient data to test the performance. (B) We could test the sensitivity of the proposed model using two sliding windows.
We implemented the proposed method by using MATLAB with the tensor_toolbox for CP-APR decomposition-based models,29 and we used Python to implement other models. We also applied the SMA and EWMA model with periods of 3 and 5 months to forecast the fall incidents as the baseline. Determination of the rank of tensor decomposition is still an open problem,30 so we evaluated the performance with different rank for tensor decompositions and presented the results with rank equal to 10, 20 and 30. This is widely used in tensor-based machine learning models, because the higher accuracy of approximation does not necessarily lead to better prediction performance.24
To evaluate the capability of the proposed models in predicting the risk of fall incident of specific locations, we conducted two sets of experiments. First, we used the models to predict whether there would be fall incidents (true or false). Second, we used the models to predict the actual number of fall incidents. The first experiment is very practical for clinical decision making, as healthcare providers usually care about which locations should be taken care of. The second experiment, though still practical, is less conclusive as there are still a lot of uncertainties not covered by the dataset. In addition, the experiment results demonstrated some expected results such as the bedside being the location with the high-risk for fall incidents.
Predicting whether there would be fall incidents
In the first experiment, we adopted the receiver operating characteristic (ROC) curve and the area under the curve (AUC) to evaluate the performance. ROC and AUC are widely used performance measures on continuous or ordinal scales.31 32 The ROC curve presents the complete information of all possible combinations of true-positive rate (TPR) and false-positive rate (FPR) by presenting the TPR on the vertical axis and FPR on the horizontal axis. AUC is a normalised value (between 0 and 1) measuring the area under ROC. AUC is a robust measure, which is independent of decision threshold.33 Therefore, a higher ROC curve with a larger AUC value indicates a better performance. We presented the ROC curves and AUC scores of our experiments for the two sliding windows (N=3 and N=5) in figure 6 and figure 7, respectively. We evaluated the performance with different value of the smoothing coefficient  for EWMA and presented the results with
for EWMA and presented the results with 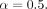
- Download figure
- Open in new tab
- Download powerpoint
ROC curves and AUC score for fall prediction (n=3). We used the data in the last 3 months (T-1, T-2 and T-3) to predict the fall incidence of a specific month T. AUC, area under the curve; CP, CANDECOMP/PARAFAC; CP-APR, CP Alternating Poisson Regression; EWMA, Exponentially Weighted Moving Average; NMTF, Non-negative Multiple Tensor Factorisation; ROC, receiver operating characteristic; SMA, simple moving average.
- Download figure
- Open in new tab
- Download powerpoint
ROC curves and AUC score for fall prediction (n=5). We used the data in the last 5 months (T-1, T-2, T-3, T-4 and T-5) to predict the fall incidence of a specific month T. AUC, area under the curve; CP, CANDECOMP/PARAFAC; CP-APR, CP Alternating Poisson Regression; EWMA, Exponentially Weighted Moving Average; NMTF, Non-negative Multiple Tensor Factorisation; ROC, receiver operating characteristic; SMA, simple moving average.
The average AUC score is shown in table 1. We found that more historical data (second column) achieved better performance than less historical data (first column). This observation is reasonable because we did not observe clear seasonality. The overall performance of the proposed CP based methods were consistently better than the baseline methods with a higher AUC value. As shown in table 1, SMA and EWMA models had identical performance, indicating that the temporal feature was without a clear trend or seasonality. For tensor-based approaches, the performances of CP-APR and NMTF based models are comparable. CP-APR-SMA and NMTF-SMA with rank 20 have better overall performance by taking both sliding window size into consideration.
Average AUC of fall incidents prediction
The ROC curve provides the visualisation for the selection of the threshold for positive outcomes (occurrence of fall incidents). From experiments with both sliding windows, we observed similar results:
If a high threshold is used for prediction, both TPR and FPR are very low for all models. This is due to the fact that with a higher threshold, only those locations where fall incidents occurred in the past few months would be selected.
If a low threshold is used for prediction, the TPR is very high with high FPR for all models. This is not acceptable with too many false predictions.
If a proper threshold in the middle is used for prediction, the performance of the proposed tensor-based models (both CP-APR and NMTF) are better than baseline models (SMA and EWMA). The results are expected because pure time series models are not able to predict fall incidents at the ‘safe’ locations with no fall record in the past few months. Unlike SMA and EWMA, the proposed methods are able to predict such incidents through exploring the structure of other dimensions.
From the comparison of ROC curves, we found that the proposed tensor-based models were able to achieve better performance than the baseline time series models in identifying high-risk locations, especially those without a record of fall incidents in the last few months.
Predicting the actual number of fall incidents
We adopted the commonly used root-mean-square error (RMSE) metric to evaluate the performance of proposed models in predicting the actual number of fall incidents, as shown in table 2. CP-APR consistently performed better than other methods, though the difference was not significant. In the previous section, NMTF presented better performance in identifying high-risk locations for fall prevention. However, RMSEs of NMTF-based models are not as good as other methods. This is partly caused by the poor fitting ratio of the decomposed tensor because of the additional non-negative constraints of NMTF and assigned rank. CP-APR-based models had a very similar RMSE as time series (SMA and EWMA) models. This is expected because in this task (predicting the actual counts), tensor-based models’ advantage of identifying the emerging risk of falls in ‘safe’ locations (those do not have previous fall record) is not significant.
RMSE for fall prediction
Conclusion
We proposed a tensor-based framework to exploit the multidimensional structure for temporal prediction of fall incidents in hospitals. We developed a set of tensor-based machine learning models to predict the occurrence of fall incidents. After evaluating the performance of the proposed models in two sets of experiments, we draw the conclusion that tensor-based models are useful tools to identify the risk of locations. However, the advantage of using tensor-based models to predict the actual number of fall incidents at specific locations is not significant.
There are several limitations of this research. First due to the highly sensitive nature of medical-related data, it is very difficult for us to obtain other datasets for cross-validation. The performance of the proposed tensor-based models was only evaluated using one dataset in this study. It is important to identify public benchmark data to further demonstrate the efficacy of the proposed models. Second, we only investigated the risk of fall incidents at specific locations (part of treatment-related factors), instead of individual patients (patient-related factors). Our proposed models have potential to be applied in individualised fall risk assessment for patients. In our ongoing research, we plan to work with nurses and hospital authorities to extract patient-level demographic information including anonymous identifier, so that we could predict the risk of falls for each patient.
The proposed fall prediction models could generate data-driven insights of patients’ fall incidence and could inform more effective and timely fall prevention programmes. This is of particular importance for Hong Kong because of its ageing population. It is also applicable for other ageing societies (like Japan). In our follow-up research, we plan to work with nurses and health authorities to develop an automatic early warning system to predict fall incidents at different locations and for individual patients.
Acknowledgments
The authors would like to thank editor and anonymous reviewers for their valuable and constructive comments.
References
Footnotes
Contributors HW and QZ designed the model and performed the experiments. ZS-YW, AK and H-YS collected the data. HW and ZS-YW performed data analysis. All authors contributed to the writing of the paper.
Funding HW and QZ are supported by the National Natural Science Foundation of China (NSFC) under grants 71402157 and 71672163 and in part by the Theme-Based Research Scheme of the Research Grants Council of Hong Kong under Grant T32-102/14N.
Competing interests None declared.
Patient consent Not required.
Ethics approval Research committee of City University of Hong Kong.
Provenance and peer review Not commissioned; externally peer reviewed.
Data sharing statement The raw hospital data are prohibited to share. The authors are happy to share the codes and hypothetical dummy data used in this research. Please email qingpeng.zhang@cityu.edu.hk.